COI: I was a co-author of the RP:P paper (but not of the response to Gilbert et al).
The first question GKPW address in their commentary is: “So how many of their [the RP:P] replication studies should we expect to have failed by chance alone?”
They estimate this, using Many Labs data, and they come to the conclusion that 65.5% can be expected to replicate, and thus the answer is 1-65.5%, or 34.5%.
This 65.5% is an important number, because it underlies the claim in their ‘oh screw it who cares about our reputation’ press release that: “the reproducibility of psychological science is quite high and, in fact, statistically indistinguishable from 100%”.
In the article, they compare another meaningless estimate of the number of successful replications in the RP:P with the 65.5 number and conclude: “Remarkably, the CIs of these estimates actually overlap the 65.5% replication rate that one would expect if every one of the original studies had reported a true effect.”
So how did GKPW get at this 65.5 number that rejects the idea that there is a reproducibility crisis in psychology? Science might not have peer reviewed this commentary (I don’t know for sure, but given the quality of the commentary, the fact that two of the authors are editors at Science, and my experience writing commentaries which are often only glanced over by editors, I’m 95% confident), but they did require the authors to share the code. I’ve added some annotations to the crucial file (see code at the bottom of this post), and you can get all the original files here. So, let's peer-review this claim ourselves.
GKPW calculated confidence intervals around all effect sizes. They then take each of the 16 studies in the Many Labs project. For each study, there are 36 replications. They take the effect size of single study at a time, and calculate how many of the remaining replications have a confidence interval around the effect size where the lower limit is larger than the effect size of the single study, or where the upper limit is smaller than the effect size. Thus, they count how many times the confidence intervals from the other studies do not contain the effect size from the single study.
As I explained in my previous blog post, they are calculating a capture percentage. The authors ‘acknowledge’ their incorrect definition of what a confidence interval is:
@StuartBuck1 @a_strezh Fair enough, but we're just employing the same metric they used, regardless of lack of precision in our language...— Stephen Pettigrew (@rink_stats) March 3, 2016
They also suggest they are just using the same measure we used in the RP:P paper. This is true, except that we didn’t suggest, anywhere in the RP:P paper, that there is a certain percentage that is ‘expected based on statistical theory’, as GKPW state. However, not hindered by any statistical knowledge, GKPW write in the supplementary material [TRIGGER WARNING]:
“OSC2015 does not provide a similar baseline for the CI replication test from Table 1, column 10, although based on statistical theory we know that 95% of replication estimates should fall within the 95% CI of the original results.”
Reading that statement physically hurts.
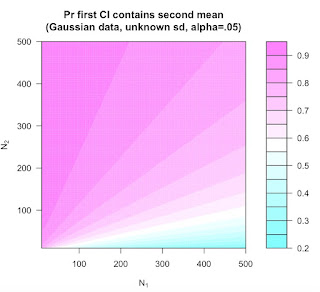
The capture percentage indicates that a single 95% confidence interval will in the long contain 83.4% of future parameters. To extend my previous blog post: There are some assumptions for this number. This percentage is only true if the sample sizes are equal (another is unbiased CI in the original studies, which is also problematic here, but not even necessary to discuss). If the replication study is larger the capture percentage is higher, and when the replication study is smaller, the capture percentage is lower. Richard Morey made a graph that plots capture percentages as a function of the difference between the sample size in the original and replication study.
The Many Labs data does not consist of 36 replications per lab, each with exactly the same sample size. Instead, sample sizes varied from 79 to 1329.
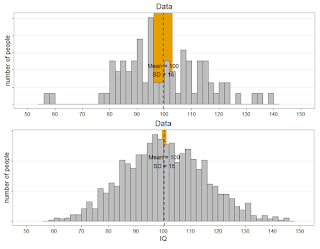
Look at the graphs below. Because the variability is much larger in the small sample (n=79, top) than in the big sample (n=1329, bottom), it's more likely that the mean in the bottom study will fall within the 95% of the top study, than it is that the mean of the top study will fall within the 95% CI of the bottom study. In an extreme case (n = 2 vs n = 100000), the mean of study n = 100000 will always fall within the 95% CI of the n = 2 study, but the mean of the n=2 study will rarely fall within the CI of the n = 100000 study, yielding a lower long-run limit of 50% for the capture percentage as calculated by GKPW.
Calculating a capture percentage across the Many Labs studies does not give an idea of what we can expect in the RP:P, if we allow some variation between studies due to 'infidelities'. The number you get says a lot about differences in sample sizes in the Many Labs study, but this can't be generalized to the RP:P. The 65.5 is a completely meaningless number with respect to what can be expected in the RP:P.
The conclusions GKPW draw based on this meaningless number, namely that “If every one of the 100 original studies that OSC attempted to replicate had described a true effect, then more than 34 of their replication studies should have failed by chance alone.” is really just complete nonsense. The statement in their press release that “the reproducibility of psychological science is quite high and, in fact, statistically indistinguishable from 100%”, based on this number, is equally meaningless.
The authors could have attempted to calculate the capture percentage for the RP:P based on the true differences in sample sizes between the original and replication studies (where 70 studies had a larger sample size, 10 the same sample size, and 20 a smaller sample size). But this would not give us the expected capture percentage, assuming all studies are true, only allowing for 'infidelities' in the replication. In addition to variation in sample sizes between original and replication studies, the capture percentage is substantially influenced by publication bias in the original studies. If we take this into account, the most probable capture percentages should be even lower. Had GKPW taken this bias into account, they would not have had to commit the world's first case of CI-hacking by only looking at the subset of 'endorsed' protocols to make the point that the 95% CI around the observed success rate for endorsed studies includes the meaningless 65.5 number.
In Uri Simonsohn’s recent blog post he writes: “the Gilbert et al. commentary opens with what appears to be an incorrectly calculated probability. One could straw-man argue against the commentary by focusing on that calculation”. I hope to have convinced the readers that focusing on this incorrectly calculated probability is not a straw man. It completely invalidates a third of their commentary, the main point they open with, and arguably the only thing that was novel about the commentary. (The other two points about power and differences between original studies and replications were discussed in the original report [even though the detailed differences between studies could not be discussed in detail due to word limitations; however, the commentary doesn’t adequately discuss this issue either]).
The use of the confidence interval interpretation of replicability in the OSC article was probably a mistake, too much based on the 'New Statistics' hype two years ago. The number is basically impossible to interpret, there is no reliable benchmark to compare it against, and it doesn't really answer any meaningful question.
But the number is very easy to misinterpret. We see this clearly in the commentary by Gilbert, King, Pettigrew and Wilson.
To conclude: How many replication studies should we expect to have failed by chance alone? My answer is 42 (and the real answer is: We can't know). Should Science follow Psychological Science's recent decision to use statistical advisors? Yes.
P.S. Marcel van Assen points out in the comments that the correct definition, and code, for the CI overlap measure were readily available in the supplement. See here, or the screenshot below:

I think the real lesson to be learned from the RP:P and the attack on the RP:P by GKPW is that typical studies in psychology, both original studies and (most) replications, simply don't collect sufficient amounts of data, as Etz & Vandekerckhove have shown in their reanalysis in http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0149794
ReplyDeleteThanks, JP. I hate to toot my own horn, but the low standard of evidence really seems to me the more important conclusion from the RPP. The fact that in almost 100 studies you can make the difference between the observed effect size and zero disappear by adding a heterogeneity assumption is just a reflection of that.
DeleteThe capture percentage and its properties was already discussed in the Supplement of the original Science article, in Appendix A4 on page 76: https://osf.io/k9rnd/.
ReplyDeleteMarcel van Assen, of the "Analysis Team" of RPP
It explains that the capture probability can vary between 0 and 1 (actually, it is .95), depending on the sample sizes of the original and replication study, even if they estimate the same true effect size. It also gives the code to estimate the expected capture probability of the RPP, which is below 0.834 because the replication sample size is often larger than the original sample size.
Thanks for pointing this out! If only Gilbert et al had read the supplement, it would have saved them a huge error.
DeleteAnd when you say 'lower than 83.4%' you mean the probability that the original studies effect size is covered by the replication effect size. I think it's more intuitive to talk about the probability that the replication effect size is captured by the CI of the original study, and this, this percentage is higher, right?
Disregarding the controversy for a brief moment, the true problem in psychological science still is the almost complete lack of reputation associated with replication. We appear to be quite different from a discipline such as physics in that sense. Attempts to raise the appreciation of research targeted at replication are few and far between. This needs to change, e.g., by authors committing to cite at least one replication study together with the original citation, or by having database engines return replicative studies together with the original works.
ReplyDeleteI completely agree. See here for a paper I co-authored on Rewarding Replications: http://pps.sagepub.com/content/7/6/608.abstract
DeleteA couple of genuine questions for you. What should the RP:P have used instead of CIs? And if Gilbert et al's commentary is meaningless, I'm left wondering, as many probably are, what the answer is to the very question you ended your post with. What replication rate would have been respectable? And what would have been consistent with a crisis?
ReplyDeleteI'm thinking that we could expect at the very least 5% of the high-fidelity studies to fail to be significant at p < .05. And maybe some subset of the remaining studies did not measure true effects, but that wouldn't necessarily be indicative of a crisis. Type I errors happen and we could expect at the very least 5% (assuming Type I error rates are not inflated). So if say ~70 studies were high fidelity and say 4 of them were Type I errors, then on a very good day ~63 of them would replicate. On a worse day (lets say not bad but not great), a fair number of the studies were likely underpowered and a few of the original studies reported effects that were not true (due to some p-hacking), that number would drop. This suggests to me the RP:P doesn't provide evidence supporting a reproducibility "crisis". That said, that doesn't mean I think Gilbert et al.s suggestion that the field at large is healthy is supported by the data either.
If you disagree, I would love to hear why, because I, like many people, am genuinely just trying to think through the implications of this. I think your writings on this issue have been a really important contribution (thank you) but I think you also could be clearer here about what you think the contribution of the RR:P was to answering this question. Gilbert et al's reasoning and use of statistics was faulty, but their exercise highlights the problems inherent in interpreting the results of the RP:P. Sure, the limitations were acknowledged in the RP:P, but still the claim was that the evidence supported a crisis, no?
It's not about taking sides but about dispassionately making sense of the evidence we have.
(And to be clear, I think the RR:P was an admirable effort and is also just one piece of evidence re: the question of whether or not there is a crisis.)
Hi Sam, maybe you should read the RP:P article. It uses at least 5 replication measures. My favorite is the authors subjective assessment - 39 out of 97 studies replicated, according to this. I don't understand how this number 'doesn't provide evidence supporting a reproducibility "crisis"'. You also seem to be assuming Type 1 error happen when all effects are true - which suggests you need to brush up on your stats.
DeleteI don't need to explain the contribution of the RP:P here - we wrote this down very nicely in the Science article.
(Not the same Sam... :P)
DeleteAs I said elsewhere already, I think the judgement whether or not there is a crisis is completely subjective. Also the use of the word 'crisis' isn't particularly helpful. And you already know my view on calling it 'reproducibility'... ;)
Either way, the RPP did a great service to the community and I can't see how anyone can in their right mind take the findings and say "Move along! Nothing to see here!" Just look at that scatter plot of effect sizes. That's pretty depressing.
I think the idea Gilbert had behind their criticism is good one. It would be useful to know how much replicability there is for typical psychology studies. I don't think it makes sense to do this across the whole field though - given how dissimilar the subfields are and how they vary in methodology (between-subject vs within-subject designs is a big difference) it would be more useful to see some subdisciplines here.
Anyway, the idea of estimating what level of replicability to expect by chance is a good one but I don't think their article really answers that question. Perhaps the correlation of effect sizes is a good measure - and how anyone can think the r=0.51 is a strong indication that all is well is beyond me.
Thanks for your reply. You seemed to take my comment as a hostile challenge rather than just honest questions following your interesting post. I'm very interested in these issues and only want to understand them better/as objectively as possible. I read the RPP when it first came out and yes, probably due for a reread, but was really wondering if you had updated thoughts on that particular question in light of this new round of discussion/analysis. You don't and that's fine. I'll reread the paper. My understanding of stats is fine - I was just suggesting that some of the original findings could have been 'honest' false positives. I could have been clearer above but what I meant was that even if 70 studies were high fidelity replication attempts, some of those were attempting to replicate honest false positives.
DeleteI agree that the subjective author assessment is quite informative. I think my main concern is that the denominator should be adjusted for this percentage to be meaningful as an estimate of reproducibility (e.g., taking into account false positives, low fidelity, etc.).
This comment has been removed by the author.
DeleteSam (the anonymous one) I'm always short to anonymous commenters here, and your post wasn't very clear. Your comments about false positives are still unclear. Can you give a numerical example of what you mean? I'm not hostile, but it's difficult to address unclear questions and my time is limited.
Delete"The use of the confidence interval interpretation of replicability in the OSC article was probably a mistake, too much based on the 'New Statistics' hype two years ago."
ReplyDeleteTotally agree. In his desire to claim the magic of CIs, Cummings uses language that could lead to such erroneous readings.
"The use of the confidence interval interpretation of replicability in the OSC article was probably a mistake, too much based on the 'New Statistics' hype two years ago."
ReplyDeleteTotally agree. In his desire to claim the magic of CIs, Cummings uses language that could lead to such erroneous readings.
The challenge for evaluating replication studies is that effect size, p-value, and statistical power are all relevant. No one parameter alone provides the whole story. My inclination is to focus on studies that have a statistical power of .90 or greater. For the RPP data (if I used the correct fields), 72 studies had a power of .90 or greater and 31 (43%) were significant (had p ≤ .05). Of the 24 studies with lower power, only 2 (8%) were significant. These do not quite match the published totals, probably due to 3 records with an unexplained X in the power field that I excluded.
ReplyDeleteI’ve been thinking recently that we can go farther than just rejecting the null hypothesis. Studies with a power of .90 or greater and a p-value of something like .25 or greater could be interpreted as supporting the null hypothesis and rejecting the alternative hypothesis. For the RPP data, this is 32 studies or 44% of the 72 studies with power of .90 or greater.
This strategy would be best implemented by calculating a p-value for the alternative hypothesis (p-value-H1) that would be the tail area for the observed outcome under the model for the alternative hypothesis that was used in the power analysis. This would be compared to the usual p-value-H0 for the null hypothesis.
P-value-H0 ≤ .05 and p-value-H1 ≥ .25 would be strong evidence supporting the alternative hypothesis.
P-value-H0 ≥ .25 and p-value-H1 ≤ .05 would be strong evidence supporting the null hypothesis.
P-value-H0 ≤ .05 and p-value-H1 < .25 would be tentative support for the alternative hypothesis, but an intermediate model or the null hypothesis may be true.
P-value-H0 < .25 and p-value-H1 ≤ .05 would be tentative support for the null hypothesis, but an intermediate model or the alternative hypothesis may be true.
This approach explicitly and symmetrically compares the study outcome with both the null and alternative models that were used in the power analysis. For the binomial case I have been exploring with power of .90, the criteria for .25 makes p-values in the range of .05-.015 put in the tentative category. Also, studies with low power can never strongly support the null hypothesis and thus are biased. It may be appropriate to consider that the effect size that gives a power of .90 (perhaps .95) is the useful degree of resolution for producing strong evidence with a hypothesis test.
I am not sure whether my initial optimistic impressions of this strategy will hold up. Any thoughts?
This comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDelete